When emplacing a support unit, such as a brigade support battalion, on the battlefield, a commander and his staff must consider the mission, enemy, terrain and weather, troops and support available, time available, and civil considerations (METT-TC). They use their experience and training to make sense of the multiple qualitative and quantitative factors that go into evaluating each variable.
This article describes a simple Microsoft Excel spreadsheet model that will assist commanders in determining where to place support units. The goal of the spreadsheet is to minimize distances from the support unit to customer units and higher echelon supply nodes, such as railheads, ports, and transfer points, based on various weights and constraints defined by the user.
The model also includes a constraint to ensure the unit stays outside the range of enemy weapons. This can be calculated automatically in Microsoft Excel by any Soldier once the math behind the tool is established.
THE EQUATIONS
Our mathematical model can be described using the analogy of balancing a pole. Assuming uniformity of mass throughout, we can balance our pole in the middle. This is analogous to placing our support unit halfway between the upper echelon unit's supply node and the customer unit.
If we place a two-pound weight on one end of the pole, we would have to move our balance point closer to the weight in order to maintain a balance. The takeaway is that to move our unit closer to the customer, we must weigh the customer heavier than the supply node and vice versa.
In a one-dimensional case, we can find our center of mass (the x coordinate) using the following formula, where xi is the location of a node or customer, wi is the weight associated with it, and n is the number of available nodes and customers. (See equation 1)
While this is a good mental exercise to get started, our planning occurs on a two-dimensional map with both an x and a y coordinate, and we often have more than two points to consider when emplacing a support unit. Fortunately, this idea of a center of mass can be extrapolated into two dimensions with multiple points to consider.
Our ultimate goal is to choose a location that minimizes the distance from the support unit to various locations while giving greater weight to the priority locations that we want to be closer to. In mathematical parlance, we want to minimize the following function where (x,y) is the location of the support unit and wi(xi,yi) are the weights and locations associated with n, the number of various nodes and customers. You might recognize the distance equation from algebra. (See equation 2)
BUILDING THE TOOL
With this mathematical model in mind, we will build our tool in Microsoft Excel. We start building our spreadsheet by entering a nominative starting location for our support unit, along with the locations of the customer units and nodes.
We will use longitudes and latitudes for our x and y coordinates for two reasons: They are universal across the globe and not associated with a given map sheet designator, and we have well-
established functions within Microsoft Excel that determine the distance between two locations using latitude and longitude data.
We will further identify customers as the main effort (ME) or supporting effort (SE). Our supply nodes will be identified as being along the main supply route (MSR) or alternate supply route (ASR). Finally, we will list suspected enemy locations and their associated ranges.
The ME/SE and MSR/ASR designations will weigh those locations accordingly to ensure our support unit is closer to the ME and MSR than to the SE and ASR. Our spreadsheet model will also ensure our unit remains outside of the range of enemy fire.
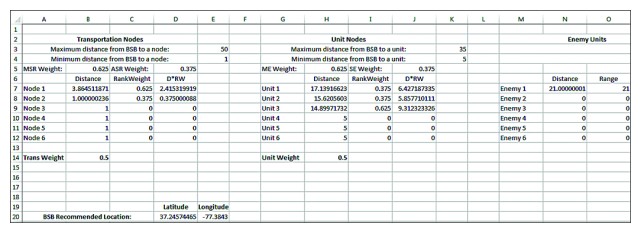
Before moving on to the calculations, we need additional inputs for our spreadsheet model. In our example (figure 1), we have weighted the supported customer units with fractions that add up to one. The ME receives five-eighths (or 0.625) of the overall value, while the SE receives three-eighths (or 0.375). We have used a similar weighting scheme for the MSR and ASR nodes.
Commanders and their staffs can adjust these weights as they see fit. We have assigned values so that the weights add up to one, but the end user can use other values to denote relative importance.
As constraints, we provide the minimum and maximum distances our support unit can be from both a customer unit and support node. We have already supplied the range of the enemy's weapons and will use them as a constraint to ensure we do not place our unit within range.
The spreadsheet model also uses global weights for both the supply nodes and customer units; however, in this example we left both equally weighted at 0.5. Global weights affect all supply nodes or customer units equally, regardless of their weights as an MSR, ASR, ME, or SE.
If a unit wishes to move its recommended location closer to either the supply nodes or customer units, they can simply adjust the global weighting. This can also be accomplished by making the constraints more restrictive.
SOLVER ADD-IN
Now that we have all the required information in our spreadsheet model, we can use Microsoft Excel's Solver Add-in to determine the optimal location for the support unit based on our input. The Solver Add-in panel uses algorithms to minimize the distance by manipulating the latitude and longitude of our support unit while considering the distance constraints previously mentioned.
For Solver to work, we must ensure that our total distance cell references the distance cells, which in turn reference the unit's location cell that we are manipulating to find our answer.
We must caution that this type of modeling can often result in more than one "optimal" location. This is because the algorithms used will find the closest location near the initial start point, but if you start elsewhere it may find a point whose summed distance is less.
A good analogy would be if you were walking in a mountain range and headed downhill to what you thought was the lowest elevation (the local minimum), but then you realized the next valley over was lower (the global minimum).
To overcome this limitation, future developments for this decision support tool will look at multiple start conditions and provide the best of the found solutions. It is important to realize that an optimal solution may not exist if every location violates one or more constraints, such as minimum distance to a customer. An inability to find a location mathematically will force us to rethink our constraints.
We are working on making the spreadsheet model easier to use while adding functions such as a relational map of all the locations. Our next step is to create a graphical user interface to automate the inputting of data into the spreadsheets. We will also automate the Solver Add-in input and output to alleviate the need for the end user to become familiar with various functions within Excel.
This method uses sound mathematical practices within an easily accessible software package to help commanders and their staffs to optimally emplace a support unit with the intent of minimizing distances. It is not intended to provide the final position. That can only be done by taking into account METT-TC through detailed staff planning.
Our tool simply takes easily identifiable quantitative data and provides a starting location. The famous mathematician George E.P. Box said that "all models are wrong, but some are useful." Anyone interested in obtaining the latest version of the tool can contact the authors by email at james.r.henry.mil@mail.mil and william.t.smith40.mil@mail.mil.
_____________________________________________________________________________________________________
Maj. James Henry is an operations research and systems analysis instructor and course director at the Army Logistics University at Fort Lee, Virginia. He holds a bachelor's degree from the U.S. Military Academy and a master's degree in operations research from George Mason University. He is a graduate of the Armor Officer Basic Course, Armor Officer Advanced Course, Combined Arms and Services Staff School, Intermediate Level Education Common Core, and the Functional Area 49 Qualification Course.
Maj. William Smith is an operations research and systems analysis instructor at the Army Logistics University. He holds a bachelor's degree in mathematics from Cameron University and a master's degree in mathematics from the Naval Postgraduate School. He is a graduate of the Ordnance Officer Basic Course, Combined Logistics Captains Career Course, Combined Arms and Services Staff School, Defense Language Institute's Russian Basic Course, and the Functional Area 49 Qualification Course.
_____________________________________________________________________________________________________
This article was published in the July-August 2014 issue of Army Sustainment magazine.
Related Links:
Browse July-August 2014 magazine
Army Sustainment Magazine Archives

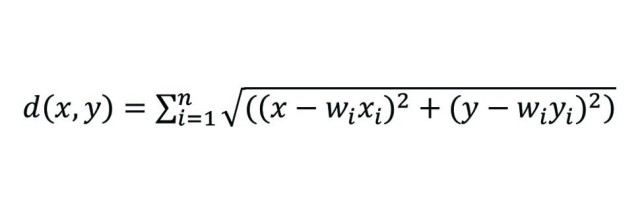



Social Sharing